Adaptive Designs are likely among the most prevalent innovative study designs, whose use is endorsed by the FDA through their Complex Innovative Trial Designs (CID) pilot meeting program from 2018[1].
An important recent publication by Price and Scott (2021) summarizing the FDA’s experience with the program reveals that all designs selected for participation thus far have employed a Bayesian framework[2]. This suggests that the Bayesian framework is proving to be the most natural and effective approach for adaptive designs.
When taking an interim look at the data during the course of a trial, frequentists traditionally use what is known as an alpha-spending function to control the type-I error when they want to stop for efficacy[3], and they compute conditional power for futility assessment or for sample size reassessment[4]. However, our experience finds several issues with this approach:
- Decisions lack a unified basis since each trial adaptation entails a separate methodology
- The selection of an appropriate alpha-spending function involves technical considerations which are difficult to communicate with sponsors and stakeholders
- Sensitivity to the choice of the alpha-spending function should be considered
- The alpha-spending approach only provides a pass/fail verdict
- Despite aiming to provide an early indication of the final result, these approaches do not employ (proper) predictive calculations.
In contrast, Bayesians use predictive modelling, possibly incorporating external/historical information, and rely on an intuitive metric (the predictive probability of trial success) for decision-making. For example:
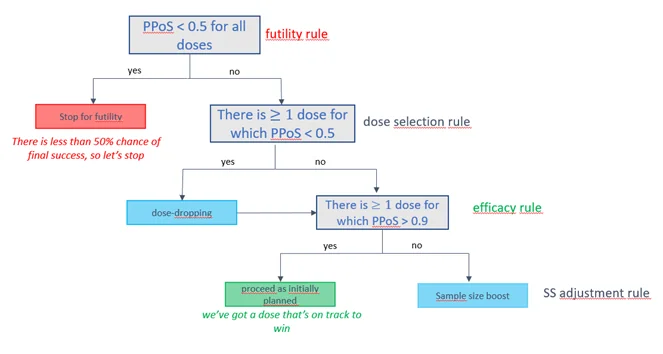
- To stop the trial early for futility if there is a high predictive probability that the treatment effect will fall below expectation
- To stop the trial early for efficacy if there is a high predictive probability that the treatment will prove effective
- To boost the sample size if the predictive probability of success is promising, but not yet conclusive.
Fictive example of an interim decision tree based on the Predictive Probability of Success (PPoS).
Inherent to the frequentist framework is its inability to assign probabilities on treatment effects, leading to less clarity in the rules. Additionally, frequentists face challenges in making proper predictive calculations and in taking all sources of variability and uncertainties into account. These shortcomings are effectively addressed by the Bayesian methodology, which our experience has shown leads to intuitive, fit-for-purpose decision rules. However, it’s important to highlight that from a regulatory perspective, these Bayesian decision rules can be fine-tuned (via simulations) to deliver acceptable frequentist properties, such as Type-I error and power5.
For example, an illustration of the calibration of Bayesian predictive decision rules can be found in a Shiny app that evaluates a new treatment’s ability to obtain complete response (CR) in Phase II oncology.
The Bayesian approach offers inherent flexibility and clarity in defining adaptive rules in a clinical trial while also preserving good frequentist properties, such as controlling the Type-1 error. Thus, we pose that it instills confidence among both sponsors and regulators.
Have you used adaptive designs for a clinical trial? What approach have you found to be most effective for your designs? We would be interested in hearing your perspective.
About the author: Marco Munda is associate director statistics at PharmaLex.
[1] Complex Innovative Trial Design Meeting Program, FDA. https://www.fda.gov/drugs/development-resources/complex-innovative-trial-design-meeting-program
[2] Price D, Scott J. The U.S. food and drug administration’s complex innovative trial design pilot meeting program: progress to date. Clinical Trials. 2021;18(6):706–710. https://pubmed.ncbi.nlm.nih.gov/34657476/
[3] DeMets D L, Lan KK. Interim analysis: the alpha spending function approach. Stat Med. 1994 Jul;13(13-14):1341-52. https://pubmed.ncbi.nlm.nih.gov/7973215/
4 Kunzmann K, Grayling M J, Lee K M, Robertson D S, Rufibach K, Wason J M S. Conditional power and friends: The why and how of (un)planned, unblinded sample size recalculations in confirmatory trials. Stat Med. 2002 Feb; 41(5): 877-890.
5 Berry S M, Carlin B P, Lee J L, Muller P. Bayesian Adaptive Methods for Clinical Trials. Chapman & Hall/CRC. 2010